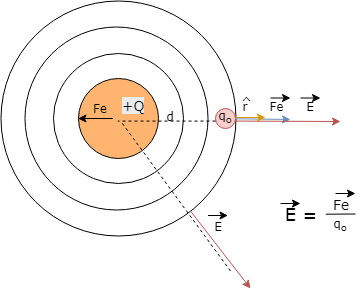
Suponha que
coloquemos numa
região do espaço uma carga denominada
de carga geradora Q. Esta carga irá
perturbar o espaço ao seu redor de tal maneira que se
colocarmos uma outra carga, chamada de carga
de prova q0, esta irá sofrer uma força que não
existiria se não houvesse a carga Q.
Assim, mesmo que não tivéssemos a carga de
prova, é razoável supor que as propriedades
deste espaço foram alteradas. É claro que só
podemos detectar essa alteração com o
auxílio da carga de prova, mas o que
queremos afirmar é que essa perturbação
independe da existência da carga de prova.
Para observarmos as propriedades do campo
elétrico, voltemos à nossa carga de prova q0 e
observemos que tipo de perturbação ela
sofre. Se existe um campo elétrico não nulo
nessa região, essa carga sofrerá uma força
de módulo, direção e sentido bem
determinados. Ao colocarmos uma grandeza
escalar (a carga elétrica) em qualquer ponto
desse campo, atuará sobre ela uma grandeza
vetorial, que é a força elétrica.
Se mudarmos apenas o sinal da carga, a força
mudará apenas de sentido, mantendo seu
módulo e direção. Uma vez feitas
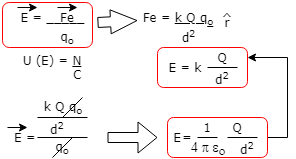
essas considerações, podemos definir como
módulo do
vetor campo elétrico a razão entre a
força que atua sobre a carga de prova
e a carga de prova, ou seja: E = F/q0.
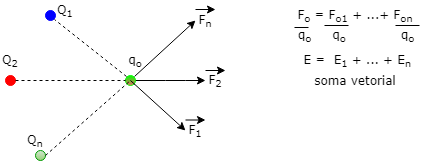
Campo elétrico
de "n" cargas
Linhas de força ou linha de campo ( cargas
pontuais).
São linhas imaginárias proposta por Faraday
com a finalidade estudar o campo elétrico.
Propriedades:
* Partem de
uma carga positiva e chegam em uma carga
negativa.
* A tangente
em qualquer ponto de uma linha de força,
indica o sentido do campo elétrico.
* A densidade
das linhas de força são proporcionais a
intensidade do campo elétrico.
* Linhas de
força nunca se cruzam.
Exercícios
Resolvidos:
1- Uma carga
elétrica puntiforme Q+ = 8 x 10-6C
está fixa em determinada região do espaço.
Considere um ponto P, de sua
vizinhança, distante 30 cm. Calcular:
a) O módulo do
campo elétrico, no ponto P.
b) O módulo da
força que atua em uma carga q+ = 2 x 10
-8C, colocada em P.
Solução:

2- Duas cargas
elétricas, Q+= 5x10-6C e q - =
2x10-6C, estão distantes 60 cm.
Determinar o(s) ponto(s) da reta que as une
onde o campo elétrico é nulo.
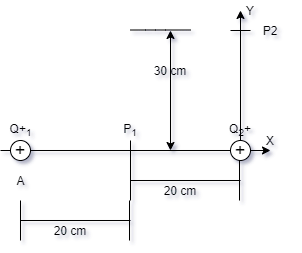
3- A figura
mostra duas cargas puntiformes, Q1+ = 3,0x10-6
C e Q2+ = 2,0x10-6C, fixas nos
pontos A e B . Calcular o módulo do campo
elétrico nos pontos P1 e P2,
indicados.
4- Qual a
intensidade de uma carga pontual que criaria
um campo elétrico de 1,00 N/C em pontos
afastados de 1,00m?
5- Duas
partículas de mesma intensidade de carga 2,0
x 10 -7C, mas de sinais
contrários, são mantidas a 15 cm uma da
outra. Quais a intensidade , a direção eo
sentido do campo elétrico localizado no
ponto médio entre as cargas?
Exercícios:
1- Uma carga
puntiforme, Q+ = 6 x10 -6 C, está
fixa em determinada região. Considere-se um
ponto P distante 50 cm dessa carga.
a) Calcular o
módulo do campo elétrico no ponto P;
b) Calcular o
módulo da força que atua em um elétron
colocado em P.
2- Duas cargas
elétricas puntiformes Q1+ = 3 x 10 -6C
e Q2+ = 6 x 10 -6C estão fixas e
distantes de 40 cm. Determinar:
a) O módulo do
campo elétrico que cada uma delas produz no
ponto em que se encontra a outra.
b) A força de
interação entre elas;
c) O(s)
ponto(s) da reta que as une nos quais o
campo elétrico é nulo.
3- Um
triângulo equilátero, de lado a. Possui duas
cargas positivas, de mesmo módulo, colocadas
nos vértices inferiores. Mostre que o módulo
do campo elétrico no vértice superior pode
ser determinado pela relação: EP
= k0Q/ a2 √3
4- Qual a
intensidade de uma carga pontual cujo campo
elétrico a uma distância de 50 cm possui
intensidade de 2,0 N/C?
5- Duas cargas
pontuais, q1 = 2,1 x 10 -8C e q2
= -4,0 q1, são fixadas com uma separação de
50 cm. Encontre o ponto ao longo da linha
reta que passa pela duas cargas no qual o
campo elétrico se anula.
6- Um elétron
é abandonado, em repouso, num ponto "0" de
um campo elétrico uniforme, conforme a
figura. Desprezando-se a força gravitacional
sobre o elétron, podemos afirmar que ele
terá:

a) movimento
oscilatório.
b) movimento
circular uniforme.
c) movimento
retilíneo uniforme.
d) movimento
retilíneo uniformemente desacelerado.
e) movimento
retilíneo uniformemente acelerado.
7- Das
afirmativas seguintes, a ERRADA é:
a) as linhas
de força de um campo elétrico são orientadas
no sentido das cargas negativas que criam o
campo;
b) o valor do
campo elétrico em um ponto onde é colocada
uma carga de prova independe do valor desta
carga de prova;
c) o valor da
força que atua sobre uma carga elétrica de
prova colocada em um campo elétrico
independe do valor da carga;
d) um elétron
colocado em repouso em um campo elétrico
tende a se deslocar em sentido contrário a
orientação das linhas de força;
e) em um campo
elétrico não uniforme, as linhas de força
não são paralelas.
8- Responda de
acordo com o código:
a) só I é
correto
b) só II é
correto
c)só III é
correto
d) I e II são
corretos
e) I e III são
corretos
I - Uma carga
elétrica não sofre ação de força elétrica se
o campo elétrico neste local for nulo.
II - Pode
existir campo elétrico sem que ai exista
força elétrica.
III- Sempre
que houver uma carga elétrica, está sofrerá
ação de força.
9- Uma
carga puntiforme Q+= 1,6x10-6C
está fixa em determinada região. Determinar:
a) O módulo do
campo elétrico, em um ponto P, distante 1,8
m da carga;
b) O modulo da
força que atua em q - = 2,0 x 10 -8C,
colocada em P.
10- Determinar
a que distância uma carga puntiforme
Q- = 3x10-6C,
produz um campo de intensidade 6,0x105
N/C.
11- Na figura
abaixo, Q1- = 2,0 x10-6C,
Q2+= 2.Q1,
l = 40cm e a = 450.
Calcular o
módulo do campo no ponto P.

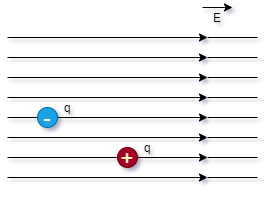
12- A figura
mostra linhas de força de um campo elétrico
e duas cargas puntiformes, colocadas em
repouso nessa campo.
a) Identificar
o campo;
b) Indicar a
direção e o sentido da força elétrica nas
cargas.
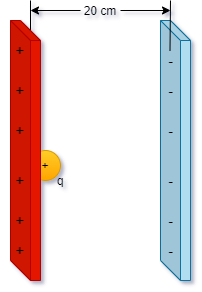
13- A
ilustração mostra duas placas, distantes 20
cm uma da outra, carregadas com carga de
sinais opostos e o campo no espaço entre
elas tem módulo E = 4,8 x 103
N/C. Uma partícula de massa m = 1,2 10-5
kg e carga q+ = 1,5 x 10-8 C é colocada, em repouso, junto à placa
positiva. Determinar:
a) as linhas
de campo entre as placas;
b) a força
sobre a partícula;
c) a
aceleração da partícula;
d) o tempo que
se gasta para tocar a placa negativa;
e) a
velocidade com que se atinge a placa
negativa;
f) a energia
cinética da partícula ao tocar a placa
negativa.
14) Uma carga
Q cria um campo elétrico E, a uma distância
d. Para que o campo elétrico seja quatro
vezes maior, a distancia da carga deve ser
igual a:
a)1/4d
b)1/2d
c)√2/2d
d)√2d
e) 2d
15- Duas
cargas elétricas de módulos iguais e sinais
opostos Q e - Q estão colocadas nos vértices
A e B de um triângulo equilátero de lado l e
originam, no vértice C, um vetor campo
elétrico E. Esse campo fica melhor
representado pelo vetor:
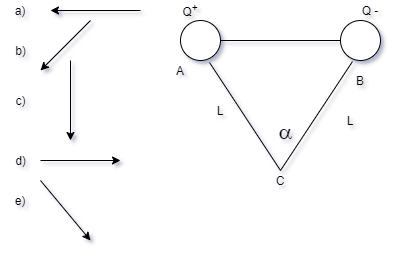
16) Para que o
campo elétrico resultante no ponto P seja
nulo, a distância d deve ser:

a) 1,25 m
b) 0,40 m
c) 0,89 m
d) 0,64 m
e) 1,56 m
17) A
intensidade de um campo elétrico em um ponto
é, numericamente, igual:
a)à força por
unidade de área.
b)à força por
unidade de distância.
c)à carga por
unidade de força.
d)à força por
unidade de carga positiva.
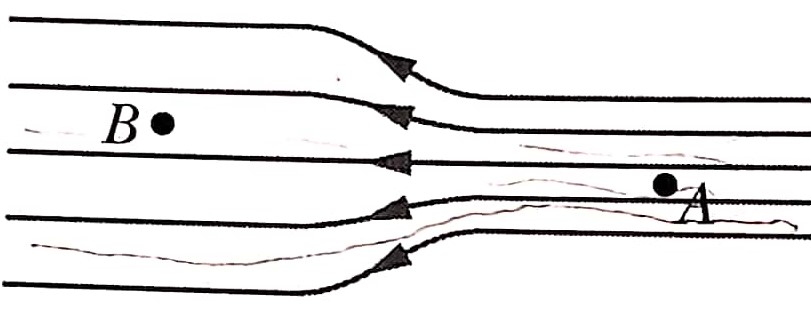
18)
Na figura abaixo as linhas de campo elétrico
na esquerda possui uma separação o que é o
dobro da separação à direita.
a)
Se a intensidade do campo em A for de
40 N/C, que força atua sobre o próton em A?
Qual a intensidade do campo em B?
19)Duas
cargas pontuais q1= 2,1 × 10
−8 C e q2 =−4,0 q1, são
fixadas com uma separação de 50 cm. Encontre
o ponto ao longo da linha reta que passa
pelas duas cargas no qual o campo elétrico
se anula.
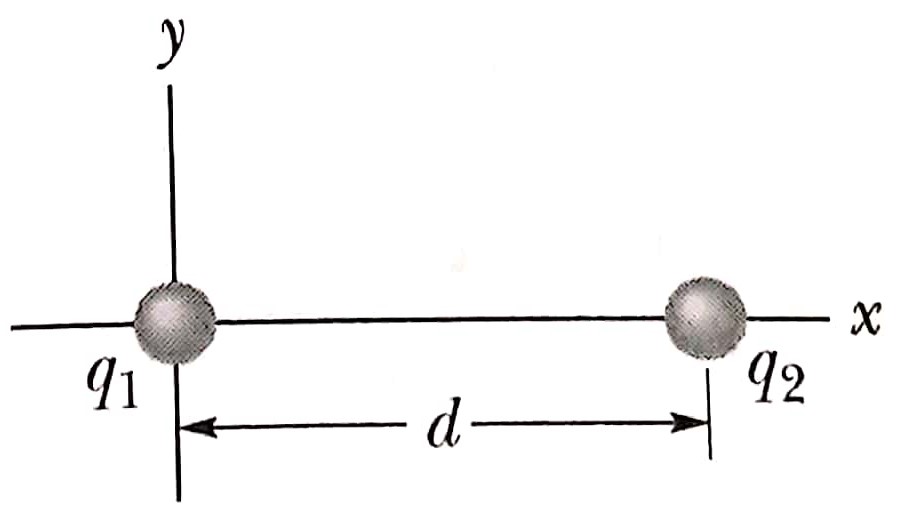
20)Na
figura abaixo duas cargas pontuais fixas q1=
−5 q e q2 =+ 2q estão separadas
por uma distância d. Localize o ponto (ou
pontos) onde o campo elétrico resultante
devido às duas cargas se anula.
21)
Com base na figura abaixo,
qual a intensidade do campo elétrico no
ponto P devido às quatro cargas pontuais
mostradas?
22)
Calcule
a direção, o sentido e a intensidade do
campo elétrico no ponto P da figura abaixo
devido às três cargas pontuais.

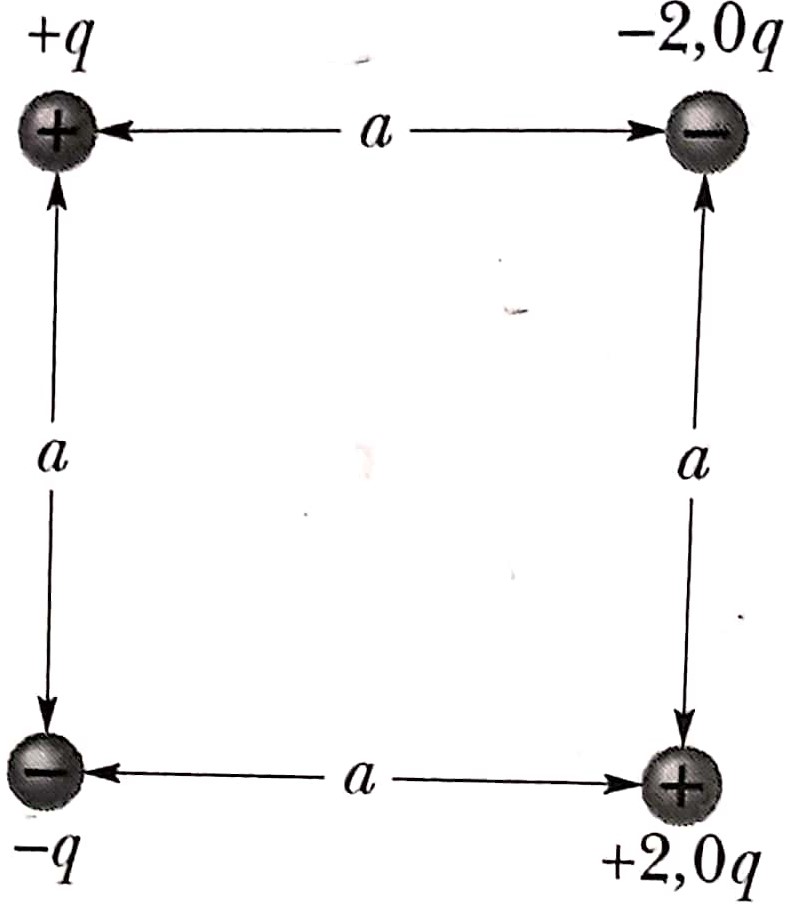
23)Quais
a intensidade, a direção e os sentido do
campo elétrico no centro do quadrado da
figura abaixo se q = 1,0 × 10 − 8
C e a = 5,0 cm ?
CAMPO ELÉTRICO
EM UMA ESFERA CONDUTORA CARREGADA
Sabemos, por
experiência, que toda a carga elétrica em
excesso, presente em qualquer corpo
condutor, distribui-se ao longo da
superfície externa, seja o corpo oco ou
maciço.
A figura
mostra uma esfera condutora, carregada
positivamente e imersa no vácuo ou ar.
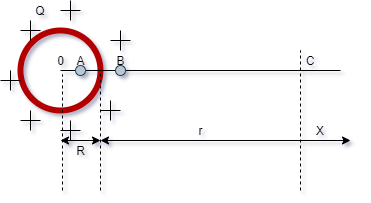
Ponto A
(Ponto no interior da esfera)
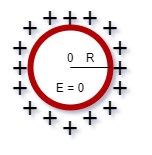
No interior da
esfera, o campo elétrico é nulo (E=0), pois,
sendo a esfera construída de material
condutor, não existe carga elétrica na
região considerada.
No interior de qualquer corpo condutor pouco
uma se som ou vetor campo elétrico é igual
ao vetor nulo.
Ponto
C (pontos Exteriores à esfera)
Para
os pontos da vizinhança da esfera a
experiência mostra que toda canga excesso
pode ser considerada como uma só carga
localizada no centro.
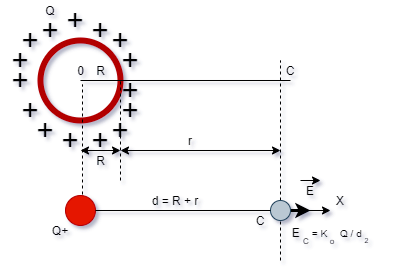
Para
pontos exteriores à esfera tudo se passa
como se toda a carga elétrica em excesso
estivesse no centro da esfera.
Ponto
B (Pontos muito próximos da superfície da
esfera)
Nos
pontos infinitamente próximos da superfície
externa da esfera, toda carga em excesso
pode ser também considerada como pertencente
à uma partícula uma puntiforme, colocada no
centro dessas esfera.
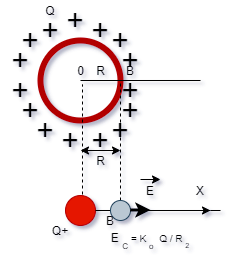
Para
pontos infinitamente próximos da superfície
externa dá esfera, tudo se passa como se
toda a carga estivesse concentrada no
centro.
Observação:
a experiência mostra que a intensidade do
vetor campo elétrico se reduz, ao passarmos
deu um ponto, infinitamente o próximo, para
um ponto efetivamente sobre a superfície da
esfera. Entretanto, como a distância desse
ponto muito próximo ao centro da esfera é
praticou praticamente igual o raio dessa
esfera podemos admitir d = R. Por essa
razão, em muitos exercícios, ao ser
mencionado o ponto sobre a superfície
externa, o ponto realmente considerado é o
infinitamente próximo.
EXERCÍCIOS RESOLVIDOS
1.
Uma esfera de raio 20 cm está carregada
positivamente com Q = +2,8 × 10 −6
C.
Tabela:
|
d (m) |
0 |
0,10 |
0,20 |
0,30 |
0,40 |
0,60 |
|
E (N/C) x 105 |
0 |
0 |
6,3 |
2,8 |
1,6 |
0,70 |
a)Completar a tabela, na qual E é o módulo
do campo elétrico e d, a distância ao
centro.
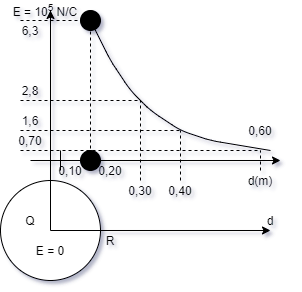
b)Traçar
o gráfico E X d utilizando os dados
numéricos da tabela.
Solução:
Os pontos d = 0 e d = 0,10cm estão situados
no interior da esfera, logo E = 0
d= 0,20m => ponto muito próximo da
superfície da esfera.
E20= ko Q/d2
E20= 9x109 . 2,8x10-6
/(0,20)2 = 6,3x105
N/C
E30= 9x109 . 2,8x10-6
/(0,30)2 = 2,8x105
N/C
E40= 9x109 . 2,8x10-6
/(0,40)2 = 1,6x105
N/C
E60= 9x109 . 2,8x10-6
/(0,60)2 = 0,70x105
N/C
2. Calcular o raio da esfera o que,
carregada com carga Q = 5,8 × 10 −6
C, produz, a 50 cm uma superfície, um campo
elétrico igual a 4,2 x 104 N/C.
solução:
E= ko Q/d2 => d2
= ko Q /E => d2
= (9x109 x 5,8x10-6
)/4,2x104
d2 = 1,24 => d = 1,11m
d = R + 0,50 => R = d - 0,50
=> R = 1,11 - 0,50 => R = 0,61m
EXERCÍCIOS DE APLICAÇÃO
1.
Uma esfera metálica de 10 cm de raio
encontra-se no vácuo eletrizada com uma
carga de 3 C. Determinar a intensidade do
campo elétrico, no seguinte os casos:
a)
a 30 cm do centro da esfera;
b) em um ponto muito próximo a superfície
das superfície externa;
c)a
5 cm do centro da esfera.
2. Duas esferas condutoras de raios a
2a portam cargas, respectivamente Q1 e Q2.
Em um ponto P, eqüidistante de seus centros,
as intensidades de seus campos elétricos são
iguais. Pode-se afirmar, então, que é a
razão q2/ q1, entre
suas cargas é
igual a:

3. Calcular o raio da esfera que, carregada
com 3,0 × 10− 6C, produz a 25 cm
da sua superfície, um campo elétrico
de intensidade 1,8 x 10 5 N/C.
4. Considere-se uma esfera condutora de raio
30 cm carregada com Q 1,5 x 10-6C.
Calcular o campo elétrico nos pontos
situados:
a) no centro da esfera;
b)a 20 cm do centro da esfera;
c)muito próximo a superfície da esfera;
d) a 10 cm da superfície da esfera;
e) a 60 cm do centro da esfera;
f) a 60 cm da superfície da esfera.
5.Considerando-se a esfera do exercício
anterior, calcular a intensidade da força
elétrica que atua em uma carga de prova
colocada a 40 cm do centro da esfera.
Sabe-se que a carga de prova é positiva e
vale 2,5 x 10 -8C.