Noções de Hidrodinâmica

 hidrodinâmica estuda os fluidos em movimento.

Equação da continuidade

Suponhamos que um líquido esteja se movendo numa tubulação qualquer, em regime uniforme e consideremos u trecho da tubulação, cuja secção longitudinal está representada na figura abaixo. Suponha que no trecho da tubulação mostrado o líquido esteja se movendo da esquerda para a direita.

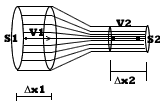
Sejam S1 e S2 as áreas das secções retas da tubulação nas regiões 1  2 e v1 e v2 as velocidades das partículas líquidas por ali passam.

Demonstra-se que

S1.v1 = S2.v2

Esta expressão é conhecida como equação da continuidade. A partir dela podemos concluir que se o diâmetro do tubo diminui, então a velocidade de escoamento do fluido no interior do tubo aumenta e vice-versa. Observa-se ainda que nas paredes mais estreitas do tubo de corrente as linhas de corrente estão mais próximas, indicando maior velocidade do fluido.

Um exemplo simples que evidencia as conclusões obtidas com a equação da continuidade, é o escoamento das águas de um rio. Nas regiões em que o rio é largo, a água flui calmamente. Entretanto, quando o rio se estreita e as margens estão mais próximas, a correnteza atinge velocidades maiores.

Vazão de volume

O produto S.v corresponde a DV/Dt. O produto S.v é chamado de vazão de volume ou simplesmente vazão. Representa-se pela letra Q. e sua unidade de medida no SI é m³/s.

Logo, a vazão mede o volume de fluido de atravessa determinada secção por unidade de tempo:                        

Q = S.v

Portanto a equação da continuidade impõe que a vazão de volume através de um tubulação é constante em qualquer secção transversal que se considere.

Teorema de Bernoulli

O teorema de Bernoulli, em essência, estabelece que a energia de um fluido em fluxo permanente, é constante ao longo do caminho descrito pelo fluido.

Essa relação nos mostra principalmente que, em uma canalização horizontal, um estrangulamento implica - pela equação da continuidade - um aumento na velocidade do fluxo e, consequentemente, uma diminuição de pressão.

Então, quanto maior é a velocidade de um fluido menor é a pressão que ele exerce.

Aplicação do Teorema de Bernoulli

Uma superfície aerodinâmica, como a asa de um avião ou um aerofólio de um carro de corrida, é desenhada de tal forma maneira que, ao se movimentar através de um fluido perturba-o de tal modo que um algumas regiões, as linhas de corrente são próximas e em outras elas não são afetadas.  figura mostra as linhas de corrente de um fluxo de ar nas proximidades de um asa de avião, mostrada em corte.

Observe que acima da asa as linhas de corrente são mais comprimidas, indicando que nessa região a velocidade do fluido é maior. Assim pelo teorema de Bernoulli. A pressão na região acima da asa deve ser menor e, portanto, existirá uma força resultante dirigida para cima (empuxo dinâmico). Esse empuxo dinâmico é geralmente chamado de sustentação.

Exemplos.:

1- O que é vazão?

2- O significa dizer que a vazão é de 50 litros/ s?

3- Uma vazão de 30 litros/s, equivale a quantos cm³/s

4- Ao chegar nos capilares, o fluxo sanguíneo tem vazão aproximadamente igual a 5 litros/min. Expresse essa vazão em c³/s

5- Na tubulação mostrada na figura escoa um liquido.

Responda:

a) A velocidade é maior em A ou em B?

b) Onde a vazão é maior?

c) A pressão é maior em A ou em B?

6- Num tubo horizontal escoa um fluido que obedece á equação da continuidade e a equação de Bernoulli. Em uma região de estrangulamento, onde a área da secção reta do tubo se d reduz á metade, a velocidade do fluido dobra e a sua pressão...............