Existem grandezas físicas que podem ser especificados fornecendo-se apenas um número. Assim por exemplo, quando dizemos que a temperatura da sala de aula é de 20ºC temos a informação completa, não sendo necessário nenhum outro dado para que a grandeza seja compreendida. Grandezas deste tipo são conhecida como grandezas escalares. Por outro lado, se tivermos estudando o deslocamento de um corpo, é necessário indicar a distância percorrida entre dois pontos, a direção e o sentido do deslocamento. A grandeza que descreve este movimento é denominada vetor.

          Vetor (termo que provem do Latim "vector = condutor")

          É um ente matemático representado por um segmento de reta orientado que tem como módulo o seu comprimento (escala), sua direção é dada pela reta suporte do Vetor, o sentido é dado através da orientação do segmento.

             Geometricamente, os vetores são representados por uma seta, cujo comprimento é chamado de módulo (escolhendo-se uma determinada escala). A direção e o sentido da seta fornecem a direção e sentido do vetor. Usualmente, ele é representado por uma letra em negrito (a, AB) ou com uma seta sobre a letra ( a  , AB .). Por outro lado, o módulo do vetor é representado apenas por uma letra ou com o vetor colocado entre barras (a, AB , etc.)

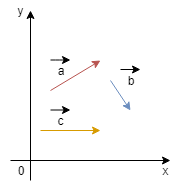
       Operações com vetores

       a) Adição Vetorial: ( Método Gráfico)

      Regra do triangulo:

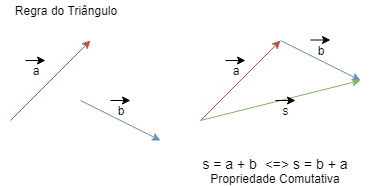
        Usando este procedimento geométrico para a adição de vetores, vemos que esta satisfaz as propriedades comutativas: a + b = b + a e associativa (a + b ) + c = a + (b + c), conforme figura abaixo.

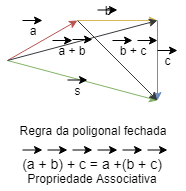
b) Subtração Vetorial:

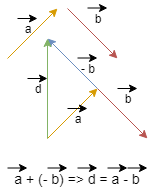
Regra do Paralelogramo

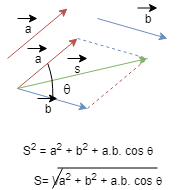
Casos Particulares (Cálculo do módulo do vetor).

1- Os vetores são ortogonais entre si. (90º).

2- Os vetores possuem mesma direção e sentido (0º).

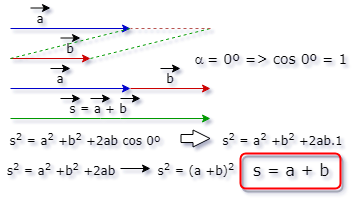
3- Os vetores possuem mesma direção e sentidos opostos (180º).

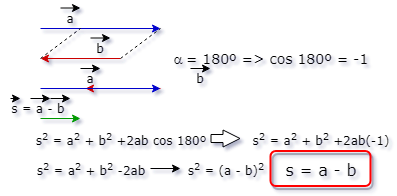
4- Componentes de um vetor.

5- Componentes na adição de um vetor.

6- Produto de um escalar por um vetor.

7- Vetores Unitários.

8- Vetor Posição.

9- Produto Escalar.

10 - Produto vetorial.

    A adição geométrica de vetores tridimensionais é muito mais difícil e para evitá-la costuma-se utilizar o método analítico, que consiste na decomposição espacial dos vetores e na manipulação individual de seus componentes.

    A decomposição de um vetor só pode se efetuada com relação a um sistema coordenadas de orientação conhecida no espaço. Considere a decomposição do vetor coordenadas de orientação conhecida no espaço. Considere a decomposição de um vetor no plano, conforme mostra a Fig., onde θ é o ângulo entre a e semi-eixo positivo x.           Dependendo do ângulo θ, as componentes podem ser positivas ou negativas. Por definição, este ângulo aumenta quando o vetor roda no sentido anti-horário. O conhecimento dos componentes de um vetor é suficiente para especificá-lo completamente, além de possibilitar a manipulação matemática simultânea de vários vetores. Muitas vezes é conveniente a introdução de um vetor de módulo unitário, chamado versor, na direção de um determinado vetor, que pode então ser escrito como a = aeˆ_a . Assim separamos o módulo do vetor (a) de sua direção e sentido ( eˆ_a ). Da mesma forma, é conveniente traçar versores paralelos aos eixos do sistema de coordenadas escolhido, como mostra a Fig. 1.7. Normalmente, no sistema de coordenadas cartesianas eles são chamados Costumamos dizer que estes versores formam uma base completa porque qualquer vetor pode ser expresso como combinação linear deles, da forma:

Exercícios:

1- Quais são (a) a componente x e (b) a componente y de um vetor “a” do plano xy que faz um ângulo de 250º no sentido anti-horário com o semieixo x positivo e tem um módulo de 7 ,3 m?

a_x = a cos q  => a_x = 7,3 cos 250^o => a_x = 7,3.(-0,34)  => a_x = -2,5 m

a_y = a sen q  => a_y = 7,3 sen 250^o => a_x = 7,3.(-0,94)  => a_y = -6,9 m

2- Um vetor deslocamento “r” no plano xy tem 15 m de comprimento e faz um ângulo q = 30º com o semieixo x positivo. Determine (a) a componente x e (b) a componente y do vetor.

a) r_x = r cos q => r_x = 15 cos 30º => r_x = 15 . 0,87 => r_x = 13 m

b) r_y = r sen q => r_y = 15 sen 30º => r_y = 15 . 0,50 => r_x = 7,5 m

3- A componente x do vetor A é -25,0 m e a componente y é + 40,0 m. (a) Qual é o módulo de A? (b) Qual é o ângulo entre a orientação de A e o semieixo x positivo?

A_x = -25,0 m    A_y = 40,0 m  A = √(-25,0)² + (40,0)²  => A = 47,2 m

tan a= 40,0/-25,0  => arco tan -15  => a = -58º   q = 180º +(-58º)

q = 122º

4- Expresse os seguintes ângulos em radianos: (a) 20,0º; (b) 50,0º; (c) 100º. Converta os seguintes ângulos para graus: (d) 0,330 rad; (e) 2,10 rad; (f) 7,70 rad.

(a) 20,0º = (20,0º) 2p rad/360^o = 0,349 rad

(b) 50,0º = (50,0º) 2p rad/360^o = 0,873 rad

(c) 100,0º = (100,0º) 2p rad/360^o = 1,75 rad

(d) 0,330 rad = (0,330 rad) 360º/2p rad = 18,9º

(e) 2,10 rad = (2,10 rad) 360º/2p rad = 120º

(f) 7,70 rad = (7,70 rad) 360º/2p rad = 441º

5- O objetivo de um navio é chegar a um porto situado 120 km ao norte do ponto de partida, mas uma tempestade inesperada o leva para um local situado 100 km a leste do ponto de partida. (a) Que distância o navio deve percorrer e (b) qual o rumo deve tomar para chegar ao destino?

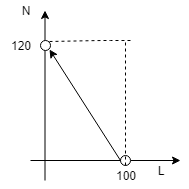
Dx = √(-100)² + 120² => Dx = 156 km

tan a = 120/-100  => tan a = -1,2  => arco tan -1,2 => a = -50,2º

q = -50,2º + 180º = 129,8º

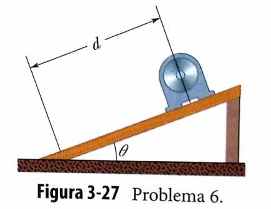
6- Na Fig. 3 - 27, uma máquina pesada é erguida com o auxílio de uma rampa que faz um ângulo q = 20,0º com a horizontal, na qual a máquina percorre uma distância d = 12,5 m. (a) Qual é a distância vertical percorrida pela máquina? (b) Qual é a distância horizontal percorrida pela máquina?

h = d sen q  => h = 12,5 sen 20,0º => h = 12,5.0,34  => h = 4,28 m

b) l = d cos q => l = 12,5 cos 20,0º => l 12,5.0,94 => l = 11,7 m

Vetores Unitários:

7- Uma pessoa caminha da seguinte forma: 3, 1 km para o norte, 2,4 km a oeste e 5,2 km para o sul. (a) Desenhe o diagrama vetorial que representa este movimento. (b) Que distância e (c) em que direção voaria um pássaro em linha reta do mesmo ponto de partida ao mesmo ponto de chegada?

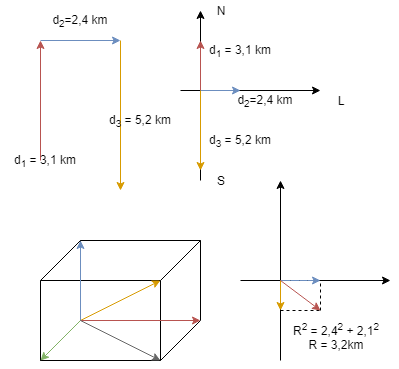
tan a = 2,1 /2,4  => tan a = 0,875  => arco tan 0,875  = > a = 41,18º

8- Dois vetores são dados por:

a = (4.0 m) î - (3,0 m) j + (1 ,0m) k

b = ( -1,0 m) i + (1,0 m) j+ (4,0 m) k.

Determine, em termos de vetores unitários, (a) a + b; (b) a - b; (c)um terceiro vetor, c, tal que a - b + c = O.

a + b = (3,0 i - 2,0 j + 5,0 k) m

a - b = (5,0 i - 4,0 j - 3,0 k) m

c = (-5,0 i + 4,0 j + 3,0 k) m

9- Determine as componentes (a) x, (b) y e (c) z da soma r dos deslocamentos c e d cujas componentes em metros em relação aos três eixos são c_x 7,4, c_y = -3,8, c_z -6,1, d_x 4,4, d_y -2,0, d_z=3,3.

a) r_x = c_x + d_x = 7,4 + 4,4 = 12 m

b) r_y = c_y +d_y = - 3,8 - 2,0 = -5,8 m

c) r_z = c_z + d_z = - 6,1 + 3,3 = -2,8 m

10- (a) Determine a soma a + b, em termos de vetores unitários, para a = (4,0 m) i + (3,0 m) j e b = ( -13,0 m) i + (7,0 m) j . Determine: (b) o módulo e (c) a orientação de a + b.

a) a+b = (-9,0 i + 10 j)  => a+b = √81 +100  => a+b = 13,45 m

q = tan-1 = 100/ -9,0  => -48º ou 132º

11- Um carro viaja 50 km para leste, 30 km para o norte e 25 km em uma direção 30° a leste do Norte. Desenhe o diagrama vetorial e determine (a) o módulo e (b) o ângulo do deslocamento do carro em relação ao ponto de partida.

12- Uma pessoa deseja chegar a um ponto que está a 3,40 km de sua localização atual, em uma direção 35,0º ao norte do Leste. As ruas por onde pode passar são todas na direção norte- sul ou na direção leste- oeste. Qual é a menor distância que a pessoa precisa percorrer para chegar ao destino?

13- Os vetores a e b da Fig. 3-28 têm o mesmo módulo, 10,0 m, e os ângulos mostrados na figura são q1 = 30º e q2 = 105º. Determine as componentes (a) x e (b) y da soma vetorial r dos dois vetores, (c) o módulo de r e (d) o ângulo que r faz com o semieixo x positivo.