Um gás se caracteriza, principalmente, pelas propriedades de poder apresentar compressão e de poder expandir-se.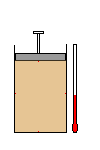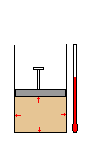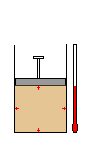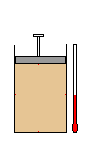

   O gás apresenta uma compressão; seu volume diminui.

   Na expansão, o volume aumenta.

Um gás ocupa todo o volume do recipiente que o contém, exercendo, sobre suas paredes, uma mesma pressão.

O gás ocupa de maneira homogênea, todo o volume do recipiente e exerce a mesma pressão sobre as suas paredes.

As principais variáveis de estado de um gás são o volume, a pressão, e a a temperatura. Isso quer dizer que , ao estudarmos o comportamento de um gás, devemos levar em consideração essas três variáveis.

Um gás ocupa o volume V, sob pressão P, na temperatura T.

Transformação ou evolução de um gás é qualquer modificação provocada em suas variáveis de estado.

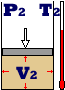
A figura mostra a transformação de um gás. Nesse caso, houve modificação nas suas três variáveis.

As condições para que um gás seja considerado ideal são:

1- o volume próprio de suas moléculas pode ser ignorado;

2- as forças de coesão entre as moléculas são desprezíveis;

3- em conseqüência das condições anteriores, um gás ideal ou perfeito não apresenta mudança de fase;

4- entre suas moléculas, não existe qualquer espécie de integração (influência), a não ser no caso de colisões, consideradas perfeitamente elásticas;

Um gás ideal, não existe qualquer interação entre suas moléculas, exceto em caso de colisões entre as mesmas e as paredes do recipiente.

Seguem rigorosamente as leis de Boyle, Gay-Lussac e Charles.

Transformação isotérmica: Uma transformação é considerada isotérmica, quando se processa com temperatura constante.

Transformação isobárica: Uma transformação é considerada isobárica, quando se processa com pressão constante, modificando-se o volume e a temperatura.

Transformação isométrica: Uma transformação é considerada isométrica ou isocórica, quando se processa com volume constante, variam pressão e temperatura.

Transformação adiabática: Uma transformação é dita adiabática, quando o gás, ao evoluir, não troca calor com o ambiente. O gás não recebe nem cede calor.

Condições normais de temperatura e pressão: (CNTP) Diremos que um gás está nas CNTP quando sua temperatura é de 0ºC e sua pressão de 1 atm.

Lei de Boyle (Isotérmica)

Consideremos uma determinada massa de um gás ideal, encerrado em um recipiente que possui um êmbolo móvel, sem atrito.

Experimentalmente, verifica-se que, variando a pressão P aplicada sobre o êmbolo, o volume V apresentará, também, uma alteração.

Desse modo, podemos construir uma tabela que mostra a relação entre P e v, sob temperatura constante.

Mantendo-se constante a temperatura de um gás, e aumentando a pressão, seu volume diminui; P a 1/V.

logo P1V1 = P2V2

Exemplos: Um gás se encontra sob pressão de 2,0 atm, em um recipiente cilíndrico de volume 50 cm³. O gás é comprimido isotermicamente até o volume alcançar 27 cm³ . Calcular a pressão nesse estado.

R...3,7 atm

2- Um gás ocupa um volume de 60 cm³ sob pressão de 1,2 atm. Calcular seu volume sob pressão de 2,8 atm e à mesma temperatura.

R..25,7 cm³    

3- Um gás tem pressão de 3 atm e ocupa determinado volume. Determinar a que pressão seu volume será reduzido à metade, em uma transformação isotérmica.

R...6 atm

Lei de Gay - Lussac (isobárica)

Um recipiente cilíndrico que contém uma determinada massa de um gás, inicialmente a 0ºC. Sobre o êmbolo é exercida uma pressão P, constante.

Aumentando-se a temperatura de um gás e mantendo-se a pressão constante, o volume também aumentará.

logo V1/V2 = T1/T2   V1/T1 = V2/T2 = cte.

Em uma mesma pressão, é constante o quociente entre o volume e a temperatura Kelvin de um gás.

Exemplo:

1- Um gás tem volume de 600 cm³ , a 27ºC, e sofre uma transformação isobárica. sabendo-se que seu volume alcançou 900 cm³ , determinar a temperatura nesse estado.

2- Um gás tem volume de 200cm³, a 127ºC. Calcular seu volume a 273ºC, sabendo-se que sofreu uma transformação isobárica.

3- A temperatura d certo volume de gás, sob pressão normal, vale 20ºC. A que temperatura seu volume será duplicado, sob mesma pressão?

4- Determinada massa de um gás está contida em um recipiente de volume 6 litros e a 0ºC. Ele sobre uma transformação isobárica e sue volume é reduzido para 3 litros. Calcular a temperatura final.

5- Um gás tem volume 0,40 m³ a uma temperatura de 127ºC. Calcular de quanto devemos reduzir sua temperatura para que seu volume alcance  0,30m³, em uma transformação isobárica.

Lei de Charles (Isométrica)

Consideremos uma certa massa de um gás, encerrada em um recipiente, como mostra a animação, vamos admitir que  Po seja a pressão inicial a 0ºC. Aquecemos o gás e mantendo o volume constante, verifica-se um acréscimo de temperatura e pressão. Esse procedimento permite determinar a relação entre pressão e temperatura de um gás, sob volume constante.

Sob volume constante, um aumento de temperatura acarreta um aumento de pressão.

logo P1/P2 = T1/T2       P1/T1 = P2/T2 = cte.

Em um mesmo volume, é constante o quociente entre a pressão e a temperatura Kelvin de um gás.

Exemplo:

1- Um gás tem pressão de 2,7 atm a 27ºC. Calcular sua pressão a 127ºC, com o mesmo volume.

R...3,6 atm

2- A temperatura de um gás é de 27ºC a sua pressão vale 1,5 atm. Determinar a temperatura que o gás deve atingir. em uma transformação isométrica, para que sua pressão se torne igual a 3,8 atm.

3- A que temperatura um gás possui pressão igual à metade da que tem a 47ºC, supondo-se o seu volume constante?

4- Um gás ocupa um volume de 4,0 litros, na temperatura de 157ºC e pressão 3,0 atm. Ele sofre uma transformação isométrica e a temperatura varia de -100ºC. Calcular a variação da pressão.

5- Sob que pressão um gás adquiri temperatura igual a u terço da que tem, com pressão de 2,7 atm, admitindo-se o seu volume constante?

Equação dos gases ideais

Em todas as transformações gasosas, consideramos uma das suas variáveis de estado constantes. Entretanto, na evolução de um gás, a pressão, o volume e a temperatura podem variar simultaneamente.

Logo:  P1V1/T1 = P2V2/T2   equação dos gases perfeitos

Exemplos:

1- Um gás tem pressão de 2,0 atm, temperatura de 127ºC e ocupa um volume de 10 litros. Determinar sua temperatura com pressão de 3,0 atm e volume de 6,0 litros.

R  87ºC

2- Sabendo-se que 15 litros de um gás estão a 27ºC e sob pressão de 2,0 atm, calcular seu volume, a 17ºC e 3,0 atm.

3- Um gás está a uma temperatura de 27ºC e tem volume V1 e uma pressão P1. Calcular a sua temperatura, caso o volume seja reduzido à metade e a pressão, triplicada.

4- Um gás a 67ºC e pressão de 1370 mm Hg, ocupa um volume de 600 cm³. Determinar que volume ocupará nas C.N.T.P.

5- Um gás a 25ºC e 760mm Hg, ocupa um volume de 125 cm³. Determine sua pressão a 80ºC e volume de 310cm³.

Estudo dos Gases Ideais – Exercícios.

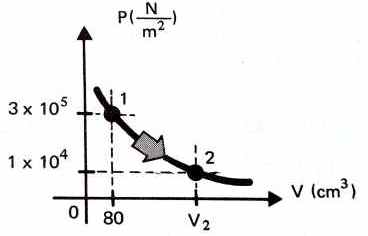
1 - O gráfico mostra a isoterma de um gás, ao passar de estado 1 para o estado 2. Calcular o volume no estado 2.

2- Um gás tem pressão de 2 atm e ocupa um certo volume. Calcular a que pressão seu volume será reduzido à terça parte, sob temperatura constante.

3- Um gás sofre uma transformação isotérmica e os valores da pressão e do volume foram tabelados.Pede-se:

1. Complete a tabela;

2. Determine o valor da constante de proporcionalidade k;

3. Construa o gráfico P x V.

4 – O gráfico representa uma transformação isobárica de um gás. Calcular:

1. O volume no estado 2;

2. A temperatura no estado 3.

5- O gráfico mostra como varia a pressão em função da temperatura, na transformação isométrica de um gás. Determinar a pressão a 0⁰C.

6- Um recipiente de volume 0,015 m³ guarda 50g de C0₂ sob pressão de 3,0 atm. Calcular:

1. O número de mols;

2. A temperatura do gas.

7- Um recipiente de volume 50 litros, contém nitrogênio (N₂). A temperatura do recipiente é de 20⁰ C e a pressão em suas paredes é de 700 mm Hg. Calcular a massa de nitrogênio contida no recipiente.

8- Um recipiente de volume 1,6 x 10⁴ cm³ contém 64 g de oxigênio, a 37⁰C. Determinar a pressão que se exerce sobre as paredes do recipiente.

9- Um recipiente de volume igual a 0 040 m³ contém 88g de C0₂ a uma temperatura de 27⁰C. Determinar:

1. A velocidade média de suas moléculas;

2. O número de moléculas no recipiente;

3. A pressão sobre as paredes do recipiente;

4. A energia cinética do gás;

5. A energia cinética média de cada molécula.

10- Um recipiente encerra determinada massa de hidrogênio (H₂) na temperatura de 27⁰C. Calcular:

1. a velocidade médias de suas moléculas;

2. a energia cinética média por molécula.

11- Uma certa massa gasosa ocupa um volume de 4,0 litros, com pressão de 1 atm. Calcular a energia cinética desse gás.

12- Um recipiente de volume igual a 5 litros contém 3 mols de C0₂. Sabendo-se que a velocidade média de suas moléculas é de 2 x 10² m/s, determinar:

1. a massa de C0₂ ;

2. a pressão sobre as paredes do recipiente;

3. a temperatura do gás;

4. a energia cinética do gás.

Equação de estado para um gás ideal: ( Equação de Clapeyron).

 1- Massa molecular de um gás (M)

A massa a molecular de um gás é a soma das massas atômicas dos átomos que constituem a sua molécula. Consideremos, por exemplo, o anidrido carbônico, (CO₂):

C = 12

O = 16  =>  CO₂  => 12 +16 + 16 = 44g

 2- Mol de um gás

É a quantidade de gás cuja massa é igual à massa molecular:

 1 mol de  CO₂ = 44g

 3- Um mol de qualquer gás contém o mesmo número de moléculas.

 1 mol => 6,02 x 10 ²³ moléculas    => número de Avogadro.

 4 - Número de Mols (n)

É o quociente entre certa massa (m) do gás e a sua massa molecular (M).

 n = massa  do gás (m)             ==>  n = m/M

       massa molecular (M)

por exemplo, 132 gramas de CO₂ corresponde a 3 mols.

n = m/M  => 132/44 = 3

 5- Nas condições normais de temperatura ( T = 273 K) e pressão (P = 1 atm), um mol de qualquer gás ocupa um volume de 22,4 litros.

 1 mol =>      =>  V = 22,4 l

  Consideremos, então a equação geral dos gases ideais:

  = k (cte)

A experiência mostra que a constante k depende, diretamente do número de mols contidos no volume ocupado pelo gás, isto é, k ∞ n.

A outra constante que transforma esta relação de proporcionalidade em uma igualdade é R (constante universal dos gases)  e podemos escrever:

     K = nR retornando a equação geral, temos : PV/T = nR

PV = nRT  (Equação de estado)

Obs.: O valor de R pode ser calculado se considerarmos as observações feitas anteriormente:

PV = nRT   = > R = PV/nT

R =  1 atm x 22,4 litros / 1 mol x 273 K = 0,082 atm.l/mol.K  ou 82 atm. cm³/mol.k

R = 1,013 x 10⁵ Pa x 22,4 x 10 ^-3 m³ / 1mol x 273K = 8,31  joule/ mol. Kelvin

Exercício: 1) Sessenta e seis gramas de CO₂ estão sobre pressão de 3,0 atm e ocupam um volume de 0,012 m³ . Determinar:

a) o número de mols;

b) a temperatura do gás.

2) Qual a massa de oxigênio (O₂ ) que devemos injetar em um recipiente de volume igual a 12 litros, para que sob pressão de 3,0 atm, apresente temperatura de 27ºC?  R = 47g

3) Um recipiente de volume 0,015 m³ guarda 50g de CO² sob pressão de 3,0 atm. Calcular:

a) o número de mols;  R = 1,14 mols.

b) a temperatura do gás.  R = 208^o C

4) Um recipiente de volume igual a 50 litros contém nitrogênio (N₂). A temperatura do recipiente é 20^o C e a pressão em suas paredes é de 700 mmHg. Calcular a massa de nitrogênio contida no recipiente.

R = 53 g

5) Um recipiente de volume 1,6 x 10⁴ cm³ contém 64 g de oxigênio, a 37^o C. Determinar a pressão que exerce sobre as paredes do recipiente.

R = 3,2 atm

6) Um recipiente de volume 2,0 litros contém C0² , sob pressão de 2,0 atm e temperatura 27^o C. Calcular:

a) o número de mols;  R = 0,16 mol

b)a massa de CO² contida no recipiente.  R = 7g

7)Cento e sessenta gramas de CO₂ estão a 127ºC e exercem uma pressão de 3,0 atm nas paredes do recipiente. Calcular o volume do recipiente.

R 54,7 L

8) O recipiente da figura abaixo é cilíndrico e o raio de sua base vale 16cm. Ele contém 88g de CO² , sob pressão de 2,5 atm e temperatura de 0º C. Calcular a altura do êmbolo em relação à base.

R = 22,3 cm

9) Se, no exercício anterior, o êmbolo for abaixado até a altura de 15 cm, calcular a pressão, sabendo-se que o termômetro marca 57^o C.

R 4,5 atm

TEORIA CINÉTICA DOS GASES

Sabemos que as moléculas de m gás possuem grande liberdade de movimento e que a trajetória de qualquer uma dessas moléculas pode ser esquematizada por uma linha quebrada, como mostra a figura que se segue.

Cada  molécula do gás executa um movimento desordenado, mas que pode ser considerado retilíneo, durante o intervalo de duas colisões.

Os segmentos, que representam deslocamentos, possuem as mais variadas extensões e direções.

A teoria cinética dos gases estuda este comportamento molecular, procurando explicar, através desse movimento desordenado e consequentes colisões, a pressão, a temperatura e a sua energia cinética.

A teoria cinética dos gases aceita o fato de que as leis da mecânica são aplicáveis ao movimento das moléculas e admite as seguintes hipóteses:

a) as moléculas possuem um movimento desordenado, com velocidade bastante variáveis, mas que permite estabelecer uma velocidade média para essas moléculas;

b) as moléculas possuem dimensões que podem ser ignoradas, em comparação com os espaços vazios existentes entre elas;

c) as colisão das moléculas entre si e com as paredes do recipiente são perfeitamente elástica. Isso significa que a energia cinética dessas moléculas se conserva.

INTERPRETAÇÃO CINÉTICA DA PRESSÃO

A pressão exercida por um gás, contido em um recipiente, é devida as inúmeras e incessantes colisões dessas moléculas contra as paredes desse recipiente. Não se pode observar o efeito individual de cada molécula, mas admite-se um efeito médio, responsável pela ação de uma força, também médias, sobre as paredes.

A relação matemática que permite determinar a pressão que um gás exerce pode ser escrita:

 onde: m = massa de gás contida no recipiente;

v = velocidade média de suas moléculas,

V = volume ocupado pelo gás.

INTERPRETAÇÃO CINÉTICA DA TEMPERATURA

Vamos procurar relacionar, agora, a temperatura (Kelvin) do gás com a velocidade media de suas moléculas.

      ==>              ==>       ==>   ==>

   ==>     ==> 

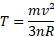
INTERPRETAÇÃO CINÉTICA DA ENERGIA CINÉTICA

Admitindo-se que cada molécula do gás tenha massa igual a m e, sendo v a velocidade média das moléculas, a energia cinética média de cada molécula será:

Sabendo que a energia cinética total do gás é a soma das energias cinéticas médias das moléculas, o que nos permite escrever:

Calor e trabalho  

O calor pode ser convertido em trabalho e que trabalho pode-se transformar em calor. A utilização dos gases e vapores nesse processo de transformação encontra aplicações na prática cotidiana.

A animação mostra um gás em uma transformação isobárica. Ao receber calor Q, seu volume aumente de V1 para V2 e, segundo a lei de Gay-Lussac, a temperatura também aumenta de T1 para T2.

A força média F é responsável pelo deslocamento H e a conseqüente variação de volume DV. A variação de volume é o volume do cilindro indicado e vale:  DV = SH.

W = P (V2 - V1)

Na expansão V2>V1 => DV >0 => w >0

Na compressão V2<V1 => DV <0 => w< 0

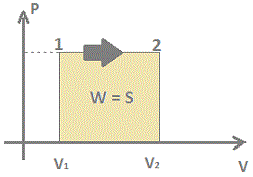
A área sob a curva do gráfico PxV, de um gás é numericamente igual ao trabalho realizado.

Exemplo:

1- Um gás, sob pressão de 1 atm, ocupa um volume de 600 cm³ a 27ºC. Ele sofre uma transformação isobárica e sua temperatura alcança 127ºC. Calcular o trabalho realizado pelo gás.

2- Um gás, sob pressão de 1,5 atm e temperatura 0ºC ocupa um volume de 400cmº. Ele sofre uma transformação isobárica e a temperatura alcança 100ºC Pede-se:

a) Calcular o trabalho realizado pelo gás;

b) construir o gráfico PxV.

3- Um gás, sob pressão de 1,8 atm e temperatura de 167ºC, ocupa um volume de 800 cm³. Ele sofre uma transformação isobárica e sua temperatura atinge 17 ºC. pede-se:

a) calcular o volume a 17ºC;

b)calcular o trabalho realizado.

PRIMEIRO PRINCÍPIO DA TERMODINÂMICA.

 Sabemos que um gás pode realizar trabalho, quando absorve determinada quantidade de calor. Entretanto, a experiência mostra que nem todo calor recebido é transformado em trabalho. Parte deste calor é utilizado pelo próprio gás e, no caso da transformação isobárica, a diferença calor - trabalho é necessária para manter a mesma pressão com volume maior. Segundo a lei de Gay-Lussac, um aumento de volume é acompanhado de um correspondente aumento de temperatura, e sabemos que variações de temperatura indicam variações de energia interna ( DU).

   Q = W + DU  onde Q = calor trocado com o meio ambiente.

W = trabalho realizado.

DU = variação da energia interna.

Exemplos.

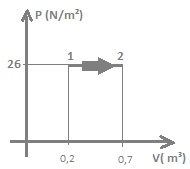
1- O gráfico acima mostra como varia o volume de um gás, sob pressão de 26 N/m², ao absorver 22 calorias.  Dados 1 cal = 4,18J

Calcular:

a) o trabalho realizado pelo gás;

b) a variação da sua energia interna.

2- Um gás ocupa um volume de 2m³ na temperatura de 73ºC, com pressão de 130 N/m². Ao absorver 975 J de energia, sofre uma transformação isobárica, e o volume alcança 5 m³. Pede-se:

a) calcular a temperatura final;

b)calcular o trabalho realizado;

c) construir o gráfico VxT (K) e PxV;

d)calcular a variação da energia interna.

3- Um gás tem volume de 0,062 m³ sob pressão de 1 atm. Ao absorver 1200 calorias, o volume passa isobaricamente para 0,084 m³. Calcular:

a) o trabalho realizado;

b) a variação da energia interna.

SEGUNDO PRINCÍPIO DA TERMODINÂMICA

De uma maneira geral, toda maquina térmica que opera em ciclos retira o calor Q1 de uma fonte quente (T1), realiza um trabalho W, e rejeita o calor Q2 ( não convertido em trabalho), denominada fonte fria.

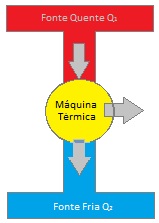
Pelo princípio da conservação da energia, Q1 = W +Q2, percebe-se que W < Q1. Isso que dizer que uma máquina não pode, na prática, transformar todo calor recebido em trabalho útil. Sempre há perdas de energia.

è impossível construir uma máquina térmica que, operando em ciclos, transforme todo o calor absorvido em trabalho.

Este princípio permite definir rendimento de uma máquina térmica.

rendimento é o quociente entre o trabalho útil realizado e o calor absorvido.

r = W/Q1

sendo W = Q1-Q2 logo  = Q1 - Q2 / Q1

r = 1 - Q2/Q1  =>  r 1 - T2/T1

Exemplos:

1- Qual é o rendimento de uma máquina térmica que retira 200 cal da fonte quente e rejeita 120 cal para fonte fria?

2- Uma máquina térmica recebe, a cada ciclo, 1000J de energia e rejeita 600J. Se ela trabalha com fonte fria de 27ºC, calcular a temperatura da fonte quente.

3- Um gás sofre uma variação isométrica, recebendo 300 cal. Determinar o trabalho que realiza e a variação da sua energia interna.

Trabalho Calor – Primeira e segunda Lei da termodinâmica – Exercícios

1. Um gás, sob pressão de 1,5 atm e temperatura de 0⁰C, ocupa um volume de 400 cm³. Ele sofre uma transformação isobárica e a temperatura alcança 100⁰C. Pede-se:

1. Calcular o trabalho realizado pelo gás;

2. Construir o gráfico P x V.

2. O gráfico representa a transformação de um gás. Pergunta-se:

1. Qual a natureza da transformação?

2. Qual o trabalho realizado.

3. Um gás sofre uma transformação isobárica, sob pressão de 1 atm, e que pode ser representada pelo gráfico. Calcular o trabalho realizado.

4. Apresentamos, nessa questão, dois gráficos, que apresentam transformações gasosas. Calcular os trabalhos realizados.

5. Um gás tem volume de 0,062 m³ sob pressão de 1 atm. Ao absorver 1200 calorias, o volume passa isobaricamente para 0,084 m³. Calcular:

1. O trabalho realizado;

2. A variação da energia interna.

6. Um gás, variando sob pressão constante e igual a 46 x 10³ N/m², apresenta uma alteração de volume, segundo o gráfico. Sabendo-se que recebeu 1130 cal, calcular:

1. O volume inicial;

2. O trabalho realizado;

3. A variação de energia interna.

7. Os gráficos a seguir mostram duas transformações gasosas. No caso A, o gás absorve 5,0J e no caso B, cede 5J. Calcular:

1. O trabalho realizado em cada caso;

2. As respectivas variações de energia interna.

8. O gráfico a seguir representa uma transformação de um gás com pressão constante e igual a 1,1 x 10⁴ N/m², e que recebeu 1302 cal. Calcular:

1. A temperatura no segundo estado;

2. O trabalho realizado;

3. A variação de energia cinética.

9. O gráfico a seguir representa uma compressão isobárica de 2 mols de um gás, que, durante a transformação, cede 8263 joules ao ambiente. Determinar:

1. A pressão do gás;

2. O volume no estado 1;

3. O trabalho realizado;

4. A variação da energia interna.

10. Determinar a quantidade de calor recebida por uma máquina térmica que realiza um trabalho de 200J com rendimento de 15% .

11. Qual o rendimento de uma máquina térmica que retira 200cal da fonte quente e rejeita 120 cal para fonte fria?

12. Determinar o rendimento de uma máquina térmica que funciona segundo o ciclo de Carnot e entre duas fontes 30⁰ C e 170⁰C.

13. Sendo de 20% o rendimento de uma máquina térmica e de 80⁰C a diferença entre as temperaturas de suas fontes, determinar a temperatura das fontes.

14. Uma máquina térmica recebe, a cada ciclo, 1000J de energia e rejeita 600J. Se ele trabalha com uma fonte fria de 27⁰C, calcular a temperatura da fonte quente.

15. Ao fornecermos 1400J de energia a um gás, seu volume passou de 10 m³ para 20 m³ . Sabendo-se que, durante o processo a pressão permaneceu constante e igual a 50 N/m², determinar:

1. O trabalho realizado pelo gás;

2. A variação da energia interna do gás.

16. Um gás sofre uma variação isométrica ( volume constante), recebendo 300 cal. Determinar o trabalho que realiza e a variação da energia interna.

17. Em uma determinada transformação, um sistema recebe 800 cal e realiza um trabalho de 1200J. Qual é a variação de energia interna?