Existem grandezas físicas que podem ser
especificados fornecendo-se apenas um número.
Assim por exemplo, quando dizemos que a
temperatura da sala de aula é de 20ºC temos a
informação completa, não sendo necessário nenhum
outro dado para que a grandeza seja
compreendida. Grandezas deste tipo são conhecida
como grandezas escalares. Por outro lado, se
tivermos estudando o deslocamento de um corpo, é
necessário indicar a distância percorrida entre
dois pontos, a direção e o sentido do
deslocamento. A grandeza que descreve este
movimento é denominada vetor.
Vetor (termo que provem do Latim "vector =
condutor")
É um ente matemático representado por um
segmento de reta orientado que tem como módulo o
seu comprimento (escala), sua direção é dada
pela reta suporte do Vetor, o sentido é dado
através da orientação do segmento. no sentido
anti-horário. O conhecimento dos componentes de
um vetor é suficiente para especificá-lo
completamente, além de possibilitar a
manipulação matemática simultânea de vários
vetores. Muitas vezes é conveniente a introdução
de um vetor de módulo unitário, chamado versor,
na direção de um determinado vetor, que pode
então
ser escrito como a = aeˆa
. Assim separamos o módulo do vetor (a) de sua
direção e sentido ( eˆa
). Da mesma forma, é conveniente traçar versores
paralelos aos eixos do sistema de coordenadas
escolhido, como mostra a Fig. 1.7. Normalmente,
no sistema de coordenadas cartesianas eles são
chamados
Costumamos dizer que estes
versores formam uma base completa porque
qualquer vetor pode ser expresso como combinação
linear deles, da forma:
São
grandezas que para ficarem perfeitamente
determinadas (compreendidas) necessitam, além do
valor numérico (módulo), a indicação de uma
direção e sentido de aplicação dessa grandeza.
Ex.: força,
deslocamento, velocidade, aceleração, campo
elétrico, etc...
11.1.
Vetor
(termo que provém do Latim “vetor = condutor”)
É um ente
matemático representado por um segmento de reta
orientado que tem como módulo o seu comprimento
(escala), sua direção é dada pela reta suporte
do Vetor, o sentido é dado através da orientação
do seguimento.

Notação:
Vetor =
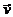 ou
v
ou
v
módulo do
vetor =
½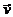 ½
ou v
½
ou v
Ex.:
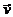 =
4u unidades
=
4u unidades
Direção: 30o
com a horizontal
Sentido: de
A para B
São vetores
que encontram-se no mesmo plano.

a) Adição Vetorial
a) Adição Vetorial
(Métodos Gráficos)
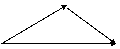 Regra do Triângulo
Regra do Triângulo







Propriedade Comutativa
Regra do Paralelogramo


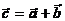

 a
a

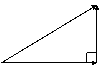
Regra do Polígono





Casos Particulares
*
 e
e
 são
perpendiculares.
são
perpendiculares.






*
 e
e
 possuem
mesma direção e sentido.
possuem
mesma direção e sentido.






*
 e
e
 possuem
mesma direção e sentidos opostos.
possuem
mesma direção e sentidos opostos.






b)
Subtração Vetorial
-









11.4. DComponentes cartesianas de um vetor.
Ax = A cos
a
Ay = A sen
a
Ay

 a
a
Ax x
Módulo Direção
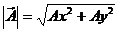


Componentes na adição de um vetor

 y
y
by



ax bx
x
Produto de um escalar por um vetor.
Produto de um escalar por um vetor.



sentido
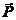 e
e
 mesmo
sentido k > 0
mesmo
sentido k > 0
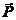 e
e
 sentidos
opostos k < 0
sentidos
opostos k < 0
Vetor unitário é um vetor adimensional que tem
módulo igual a unidade (1) e aponta numa certa
direção.
Vetor unitário é um vetor adimensional que tem
módulo igual a unidade (1) e aponta numa certa
direção.
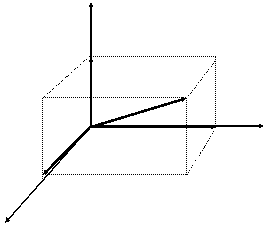 y
y
y
y


 x Ay
x Ay

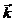 x
x
z Az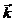 Ax
Ax



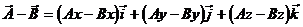
EXEMPLO:
Determine as componentes cartesianas
ortogonais e represente-as com o auxílio de
 e
e
 os
vetores:
os
vetores:
a)
 =
20N a 60o b)
=
20N a 60o b)
 =
100m/s a 90o c)
=
100m/s a 90o c)
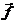 =
400kgf a 205o
=
400kgf a 205o
a)
y Fx = 20. cos 60 o
 =
20N Fx =
20. 0,5
=
20N Fx =
20. 0,5
Fx = 10 N
 Fy
Fy 60o
60o
x Fy = 20. sen 60
o
Fx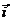 Fy = 20. 0,87
Fy = 20. 0,87
Fy = 17,3 N
 =
(10
=
(10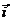 +
17,3
+
17,3 )
N
)
N
 b)
y
b)
y
 =
0
=
0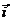 +
100
+
100
 =
100m/s
=
100m/s
 =
100
=
100 m/s
m/s
90o
x
c)
y fx = 400. cos 205o
fx = - 362,5 kgf
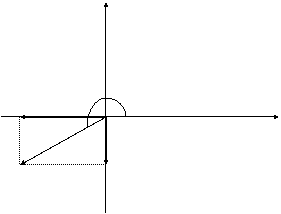 fx 205o fy = 400. sen 205 o
fx 205o fy = 400. sen 205 o
x fy = -169 kgf
fy
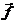 =
400kgf
=
400kgf

EXERCÍCIOS:
1. Uma pessoa anda 3km para leste e depois 4km
numa direção a 60o ao norte do leste.
Pede-se:
a) desenhe um diagrama do movimento. (1cm = 1km)
b) Indique o deslocamento resultante e seu
módulo. (M. Gráfico)
c) Calcule o módulo do vetor resultante através
da equação do paralelogramo.
2. Determina a resultante de forças representado
na figura.
y
F1=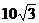 N
N
F2 =
3N 30o

60o
F3 = 2N
3. Dados dois vetores
 m
e
m
e  m.
Pede-se:
m.
Pede-se:
a)  b)
b) 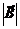 c)
c) 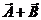 (módulo
e direção) d)
(módulo
e direção) d)
 (módulo
e direção)
(módulo
e direção)